ABSTRACT Previous studies on chewing frequency across animal species have focused on finding a single universal scaling law. Controversy between the different models has been aroused without

elucidating the variations in chewing frequency. In the present study we show that vigorous chewing is limited by the maximum force of muscle, so that the upper chewing frequency scales as

the −1/3 power of body mass for large animals and as a constant frequency for small animals. On the other hand, gentle chewing to mix food uniformly without excess of saliva describes the

lower limit of chewing frequency, scaling approximately as the −1/6 power of body mass. These physical constraints frame the −1/4 power law classically inferred from allometry of animal

TAPIRS, WITH IMPLICATIONS FOR THE DIETARY ECOLOGY OF EARLY HOMININS Article Open access 01 June 2020 INGESTIVE BEHAVIORS IN BEARDED CAPUCHINS (_SAPAJUS LIBIDINOSUS_) Article Open access 30

November 2020 INTRODUCTION In 1944, Erwin Schrödinger argued that organisms have evolved to avoid decay and to stay alive “by eating, drinking, breathing and (in the case of plants)

assimilating”1. In the animal kingdom, eating is an essential activity of organisms from mycoplasmas to blue whales over twenty orders of magnitude in body size2. Food chewing has evolved

over millions of years as a solution to increase digestive efficiency and achieve high levels of metabolic activities in terrestrial mammals (as compared to other vertebrates of similar

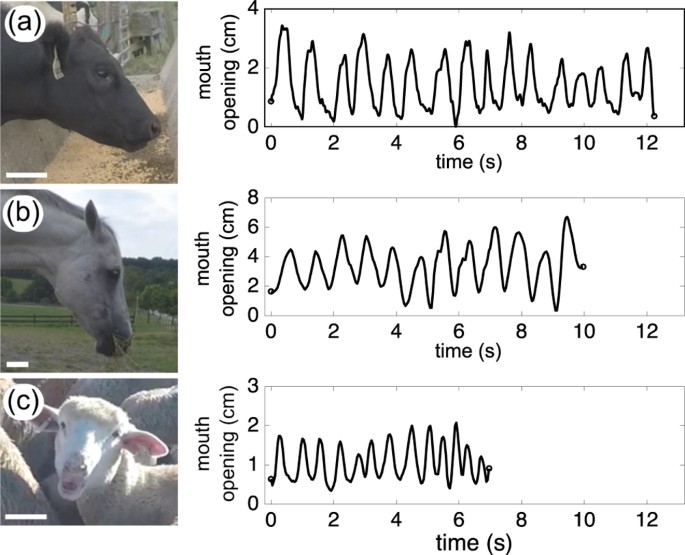
masses), thereby setting the stage for endothermic temperature physiology and the fascinating diversification in mammals seen today3 (see examples of a cow, a horse, and sheep in Fig. 1).

Fortelius proposed that the volume of food per chew is proportional to the animal mass and that the food per unit time is proportional to the metabolic rate4, which scales as the 3/4 power

of body mass according to Kleiber’s law5,6,7. As a consequence, the chewing frequency should be proportional to the −1/4 power of body mass (_Mf_chew ~ _M_3/4). This model was supported by

experimental observations of _f_chew ~ _M_−0.20 4. Later, Druzinsky observed a different scaling _f_chew ~ _M_−0.13 by including small animals over three orders of magnitude in body mass,

and concluded that the chewing frequency might not directly be related to the metabolic rate8. Quite recently, Gerstner _et al_. have highlighted that all previous theoretical models have

failed to describe correctly the contemporary data of chewing frequencies, which are midway between the previous two, i.e. _f_chew ~ _M_−0.15 in ref. 9. This scaling seems to emerge from a

scenario of optimal chewing where the chewing power is maximized (i.e. where the energy per chew is maximized while the time to chew is minimized). Based on Hill’s law, the muscle force and

contraction speed are inversely correlated, so that the peak power is not simply achieved at the maximal force10. The peak power has been studied in the context of animal locomotion11,12,

where the preferred speed of locomotion (_V_) lies between the 0.17 and 0.22 power of body mass. In analogy to the chewing motion, by assuming that the speed of muscle contraction is

proportional to the motion speed and by assuming an amplitude of motion proportional to the jaw length (with _L_jaw ~ _M_1/3 as precised in the present article), the chewing frequency

_f_chew ~ _V/L_jaw is expected to lie between the −0.16 and −0.11 power of body mass. Some recent studies also have suggested that the chewing frequency could match the jaw’s natural

resonance frequency using the analogy of a pendulum (; see e.g. refs 13,14 for primates and dogs). However, a gravity-driven chewing model is known to be biomechanically unrealistic

regardless of the best fit to experimental observations14. In summary, previous studies on chewing frequency have focused only on finding a single scaling; _f_chew ~ _M_−0.20 for large

animals4, _f_chew ~ _M_−0.13 after including small animals8, _f_chew ~ _M_−0.15 for the largest data-set9 and finally _f_chew ~ _M_−1/6 based on pendulum-type movement of jaws13,14. Also,

frequency variations were considered as statistical noise or randomness, which has generated a variety of scaling laws and aroused controversy between different models. Therefore, in

contrast to the previous studies predicting a single functional relation between the chewing frequency and animal weight, in this study we determine the range of frequencies where animals

can chew their food. RESULTS EXPERIMENTAL DATA OF THE CHEWING FREQUENCY Measurements of chewing frequency are reported on Fig. 2 over six orders of magnitude of animal mass. Black circles

denote data that we measured from Virginia Tech farms, boxed rectangles are data that we estimated from online sources (see Materials and Methods) and triangles are measurements reported

by8,9,13,14,15. We denote carnivores, herbivores, and omnivores with red, green, and blue colors, respectively. In the following sections, we focus on the role of saliva and muscles to

explain the observed discrepancies. THE SALIVA LIMIT Saliva is essential to chew, taste, and digest food. It lubricates between the mouth and food contents and between food contents

themselves. Also, saliva enhances taste and digestion through bio-chemical processes. Salivary flow rate is known to vary depending on situations. For example, saliva is secreted at a very

low flow rate when animals sleep or rest. However, when the salivary glands are mechanically stimulated during chewing, the saliva flow rate significantly increases. Animals have four pairs

of major salivary glands connected to the oral cavity. Figure 3(a) shows the saliva flow rate of various animals previously measured in refs 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27,

28, 29, 30, 31. We found an approximate power law for the flow rate of saliva _Q_ ~ (4.8 × 10−6 kg1/6/s) _M_5/6 (best fit with a 0.87 power, _r_2 = 0.90, _n_ = 30, _p_ < 0.0001, 95%

confidence interval: 0.79 to 1.00, see Fig. 3(a)). To efficiently mix saliva with food, the total amount of secreted saliva should be on the same order of magnitude with food amount within

two consecutive swallows (which may include several chewing cycles) and should not exceed it. Therefore, based on the assumption that the saliva amount over the chewing period is close to

the volume of oral cavity, we have Here, _T_swallow is the chewing time, equivalent to the number of chewing cycle times the inverse of chewing frequency, and _V_oral is the volume of the

oral cavity. The total number of chewing cycles before swallowing is measured to be 15.9 ± 5.1 over 21 primate species with four orders of magnitude of different body masses (this conclusion

can be reached from the data measured by ref. 32). This number of cycles seems to be set by geometric relations: if we assume that the food is crunched into two pieces at every chewing

motion, the number of chewing cycle should increase until the initial volume of food () is ground to the size of upper esophageal sphincter for further digesting. Therefore, the total number

of chewing cycles before swallowing is estimated as where _D_esophagus is the diameter of the food pipe (esophagus). In this expression, both _L_jaw and _D_esophagus presumably scale

isometrically with body mass, giving _N_chew ≃ 101 regardless of body mass. In case of humans33, _L_jaw/_D_esophagus ≃ 20 and equation (2) becomes _N_chew ≃ 13, which is close to the

observations in primate species. This approach only gives the order of magnitude, further details are provided in ref. 34. _V_oral is the volume of the oral cavity, assumed to scale as the

cube of jaw length (_V_oral ≃ 4π(_L_jaw/2)3/3). The jaw length _L_jaw is found to be _L_jaw ≃ (5.0 × 10−2 m/kg1/3) _M_1/3 (best fit with a 0.37 power, _r__2_ = 0.92, _n_ = 95, _p_ < 

0.0001, 95% confidence interval: 0.35 to 0.40, see Fig. 3(b)). Therefore, the chewing frequency for saliva mixing verifies In Fig. 2, all data stand above this limit, which supports the

validation of our model based on saliva mixing. Also, the exponent −1/6 is the same as a previously proposed model of pendulum-type chewing14, but based on different physics (our model is

independent of gravity and head rotation). THE MUSCLE LIMITS The highest frequency of food chewing is presumably related to maximal muscle performance. Rhythmic chewing motion is modeled as

a spring-like oscillation operated by the masseter muscles (Fig. 4). Based on ref. 14, the natural frequency of chewing for primates can be expressed as where the masseter lever distance,

_L_masseter, is defined as the length between the masseter muscle and the jaw joint. Ross _et al_.14 showed that the masseter lever distance is about a half of the jaw length. First, we

assume the jaw mass (_m_jaw) to be _ρ_tissue_V_oral with _ρ_tissue ≃ 103 kg/m3 and , and the spring constant (_K_muscle) to be _F_muscle/(_L_jaw/2). Here, _L_jaw ≃ (5.0×10−2 m/kg1/3) _M_1/3

as shown in the previous section. The maximum muscle force is proportional to the physiologic cross-sectional area (abbreviated as PCSA) of jaw muscle _A_muscle ≃ (3.9×10−4 m2/kg2/3)_M_2/3

(best fit with a 0.73 power, _r_2 = 0.71, _n_ = 91, _p_ < 0.0001, 95% confidence interval: 0.63 to 0.82, see Fig. 3(c)). Also, the maximum muscle force per unit area,  N/m2 is used35.

Finally, by combining all of the above values and relations, the chewing frequency verifies In addition, muscles are intrinsically limited in terms of contraction speed. Muscles typically

consist of sarcomeres in series, of individual length _l_s ≃ 2.5 _μ_m, all being shortened at the same speed (with ATP hydrolysis), and the maximal contraction speed relative to length

should be essentially independent of body size: _v_s ≃ 19 _μ_m/sarcomere/s36,37,38. Therefore we can assume that the frequency of jaw muscles also verifies This intrinsic frequency

presumably sets the upper limit of chewing frequency for small animals as observed in Fig. 2. For large animals heavier than 20 kg, the scaling of equation (5) prevails. DISCUSSION In

contrast to the previous studies predicting a single scaling for the chewing frequency, here we have determined the range of chewing frequencies where terrestrial mammals can chew their

food. Figure 2 shows that chewing behaviors are described by our proposed physical limits. The upper chewing frequency seems essentially limited by muscular actuation, and the lower chewing

frequency is limited by mixing food with the right amount of saliva (i.e. without unnecessary excess) during a finite number of chews before swallowing. The variations of chewing frequency

in Fig. 2 could be primarily due to the type of food14,31,39. The upper limit in frequency derived in equation (5) is independent of the food type by essence. It can be considered as the

inertial limit of the jaw motion. To take into account the role of food elasticity, we assume that the chewing power _P_max developed by an animal to granulate food scales as its metabolic

rate. Then, we postulate that this power is proportional to _EA_dental_f_chew_L_jaw, where _E_ is the elastic modulus of the food and _A_dental is the dental occlusion area, scaled

isometrically with body mass (see ref. 32 and its references). As a consequence, we find _f_chew ~ _E_−1_M_−1/4. This contribution is needed when the food rigidity _EL_jaw is greater than

the muscle rigidity _K_muscle. In case of humans, we have _K_muscle ≃ 106 N/m, thus the inertial model is valid when food elastic modulus does not exceed 10 MPa. Also, for large animals,

chewing frequency is less affected by the food properties since their muscle rigidity is significantly larger than the food elasticity (_K_muscle ~ _M_1/3). In summary, the domain of chewing

frequency is limited by several inequalities, not by a single power law. We find that chewing becomes an irrelevant mechanism if the minimal frequency required by efficient saliva mixing

(~_M_−1/6) is higher than the maximal frequency at which muscles can be actuated, i.e. for animals heavier than 107 kg or lighter than 10−5 kg. Therefore our work may also contribute to

understanding why we do not observe terrestrial mammals as heavy as the mega sauropods (dinosaurs extinct approximately 100 millions years ago) of mass ~100 tons40,41,42, because their

chewing frequencies would be presumably confined by the inertial and saliva-based limits in a small frequency range (0.2–0.5 Hz). Similarly, one cannot find any terrestrial mammal

approaching the smallest weight limit, since the lightest contemporary mammal (Etruscan shrew) weighs about 1 g. More generally, the upper limit for jaw oscillation frequency could be tested

on rumination or even teeth-chattering. For future work, it would be interesting to consider how the chopping of soft and tough food by “our” teeth (which by itself requires energy) affects

the physical limits of the chewing frequency. MATERIALS AND METHODS This study was carried out during the regular feeding times and animals were weighted during the maintenance period with

the consents of farm managers. This study plan was discussed with, and approved by the Institutional Animal Care & Use Committee (IACUC) of Virginia Tech. All experiments presented in

this manuscript were performed in accordance with relevant guidelines and regulations. STUDY SUBJECTS Cows (_Bos taurus_), horses (_Equus caballus_) and sheep (_Ovis aries_) at Virginia Tech

farms were chosen as subjects (Fig. 1 and supplementary videos). These animals were raised in good health and their body masses were measured within one month after recording chewing

motion. A total of twenty animals were used for the analysis (nine cows, three horses and eight sheep). Individual animals were fed with daily food by their farm managers (cows and sheep

with grain, and horses with dry hay). Then, chewing sequences were videotaped using two GoPro cameras at 120 fps. The chewing motion of these animals was analyzed from frame-by-frame image

sequences. We excluded the chewing motion while animals were collecting or ruminating food. A chewing period was measured by the time interval between consecutive jaw closing moments, and

the chewing frequency, _f_chew, is defined as the inverse of this chewing period. At least five chewing cycles were analyzed for individual animals. In addition to these field measurements,

we collected 86 videos of animals chewing food from online databases. We selected videos based on clear oscillatory chewing motions of animal. We paid special attention to finding animal

species not locally accessible. Also, to get reliable statistics, the selected videos contain at least three cyclic chewing motions of each animal without a break. We determined a range of

animal body mass from literature and encyclopedia. All the videos and the range of body mass are listed in the Tables S1, S2 and S3 (see electronic supplementary material). ADDITIONAL

INFORMATION HOW TO CITE THIS ARTICLE: Virot, E. _et al_. Physics of chewing in terrestrial mammals. _Sci. Rep._ 7, 43967; doi: 10.1038/srep43967 (2017). PUBLISHER'S NOTE: Springer

Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. REFERENCES * Schrödinger, E. _What is life?_(Cambridge University Press, 1944).

* McMahon, T. A. & Bonner, J. T. _On size and life_(Scientific American Library, 1983). * Ungar, P. S. _Mammal Teeth: Origin, Evolution, and Diversity_(Johns Hopkins Univ. Press,

Baltimore, 2010). * Fortelius, M. Isometric scaling of mammalian cheek teeth is also true metabolic scaling. _Mem. Mus. natn. Hist. nat._ 53, 459–462 (1988). Google Scholar  * Kleiber. M.

Body size and metabolism. _Hilgardia_ 6, 315–353 (1932). Article  CAS  Google Scholar  * McMahon, T. Size and Shape in Biology. _Science_ 179, 1201–1204 (1973). Article  CAS  ADS  Google

Scholar  * Brown J. H. & West G. B. _Scaling and Biology_ 87–112 (Oxford Univ. Press, 2000). * Druzinsky, R. E. The time allometry of mammalian chewing movements, chewing frequency

scales with body mass in mammals. _J. Theor. Biol._ 160, 427–440 (1993). Article  CAS  Google Scholar  * Gerstner, G. E. & Gerstein, J. B. Chewing rate allometry among mammals. _J.

Mammal._ 89, 1020–1030 (2008). Article  Google Scholar  * Hill, A. V. The heat of shortening and the dynamic constants of muscles. _P. Roy. Soc. Lond. B Bio._ 126, 136–195 (1938). Article 

ADS  Google Scholar  * McMahon, T. A. _Muscles, Reflexes, and Locomotion_(Princeton Univ. Press, 1984). * Heglund, N. C. & Taylor, C. R. Impact of meat and lower palaeolithic food

processing techniques on chewing in humans. _J. Exp. Biol._ 138, 301–318 (1988). CAS  PubMed  Google Scholar  * Gerstner G. E., Cooper, M. & Helvie P. Chewing rates among domestic dog

breeds. _J. Exp. Biol._ 213, 2266–2272 (2010). Article  Google Scholar  * Ross, C. F. et al. Scaling of Chew Cycle Duration in Primates. _Am. J. Phys. Anthropol._ 138, 30–44 (2009). Article

  Google Scholar  * Fortelius, M. Ungulate cheek teeth, developmental, functional, and evolutionary interrelations. _Acta Zool. Fennica_ 180, 1–76 (1985). Google Scholar  * Kay, R. N. The

rate of flow and composition of various salivary secretions in sheep and calves. _J. Physiol._ 150, 515–537 (1960). Article  CAS  Google Scholar  * Watanabe, S. & Dawes, C. A comparison

of the effects of tasting and chewing foods on the flow rate of whole saliva in man. _Arch. Oral Biol._ 33, 761–764 (1988). Article  CAS  Google Scholar  * Sassaki, K. T. et al.

Neuroendocrine alterations impair enamel mineralization, tooth eruption and saliva in rats. _Pesqui. Odontol. Bras._ 17, 5–10 (2003). Article  Google Scholar  * Wang, S. et al. The miniature

pig: a useful large animal model for dental and orofacial research. _Oral Dis._ 13, 530–537 (2007). Article  CAS  Google Scholar  * Gurnsey, M. P., Jones, W. T. & Reid, C. S. W. A

method for investigating salivation in cattle using pilocarpine as a sialagogue. _New Zeal. J. Agr. Res._ 23, 33–41 (1980). Article  Google Scholar  * Chauncey, H. H., Henriques, B. L. &

Tanzer, J. M. Comparative enzyme activity of saliva from the sheep, hog, dog, rabbit, rat, and human. _Arch. Oral Biol._ 8, 615–627 (1963). Article  CAS  Google Scholar  * Meurman, J. H.

& Rantonen, P. Salivary flow rate, buffering capacity, and yeast counts in 187 consecutive adult patients from Kuopio, Finland. _Scand. J. Dent. Res._ 102, 229–234 (1994). CAS  PubMed 

Google Scholar  * Vissink, A. A functional and chemical study of radiation effects on rat parotid and submandibular/sublingual glands. _Radiat. Res._ 124, 259–265 (1990). Article  CAS  ADS 

Google Scholar  * Anderson, D. J., Hector, M. P. & Linder, R. W. The possible relation between mastication and parotid secretion in the rabbit. _J. Physiol._ 364, 19–29 (1985). Article 

CAS  Google Scholar  * Gjorstrup, P. Parotid secretion of fluid and amylase in rabbits during feeding. _J. Physiol_. 309, 101–116 (1980). Article  CAS  Google Scholar  * Enwonwu, C. O.,

Sawaris, P. & Chanaud, N. Effect of marginal ascorbic acid deficiency on saliva level of cortisol in the guinea pig. _Arch. Oral Biol._ 737, 515–537 (1995). Google Scholar  * Horowitz,

M. & Meiri, U. Thermoregulatory activity in the rat: effects of hypohydration, hypovolemia and hypertonicity and their interaction with short-term heat acclimation. _Comp. Biochem.

Physiol._ 82, 577–582 (1985). Article  CAS  Google Scholar  * Isomura, E. T. et al. Saliva Secretion Stimulated by Grafted Nerve in Submandibular Gland Allograft in Dogs. _J. Physiol._ 83,

759–763 (2007). Google Scholar  * Maekawa, M., Beauchemin, K. A. & Christensen, D. A. Effect of concentrate level and feeding management on chewing activities, saliva production, and

ruminal pH of lactating dairy cows. _J. Dairy Sci._ 85, 1165–1175 (2002). Article  CAS  Google Scholar  * Beauchemin, K. A. et al. Salivary Secretion During Meals in Lactating Dairy Cattle.

_J. Dairy Sci._ 91, 2077–2081 (2008). Article  CAS  Google Scholar  * Gaviao, M. B. D. Chewing behavior and salivary secretion. _Eur. J. Oral Sci._ 112, 19–24 (2004). Article  Google Scholar

  * Ross, C. F. et al. Ecological consequences of scaling of chew cycle duration and daily feeding time in Primates. _J. Human Evol._ 56, 570–585 (2009). Article  Google Scholar  * Yip, H.

T., Leonard, R. & Kendall, K. A. _Laryngoscope_ 116, 93–96 (2006). Article  Google Scholar  * Alexander, R. McN. Engineering approaches to chewing and digestion. _Science Progress_ 82,

171–184 (1999). Article  Google Scholar  * Ikai, M. & Fukunaga, T. Calculation of Muscle Strength per Unit Cross-Sectional Area of Human Muscle by Means of Ultrasonic Measurement. _Int.

Z. angew. Physiol. einschl. Arbeitsphysiol._ 26, 26–32 (1968). CAS  Google Scholar  * Weijs, W. A. & van der Wielen-Drent, T. K. The relationship between sarcomere length and activation

pattern in the rabbit masseter muscle. _Arch. Oral Biol._ 28, 307–15 (1983). Article  CAS  Google Scholar  * Burkholder, T. J. & Lieber, R. L. Sarcomere length operating range of

vertebrate muscles during movement. _J. Exp. Biol._ 204, 1529–1536 (2001). CAS  PubMed  Google Scholar  * Vogel, S. Living in a physical world, III Getting up to speed. _J. Biosci._ 30,

303–312 (2005). Article  Google Scholar  * Zink, K. D. & Lieberman, D. E. Impact of meat and lower palaeolithic food processing techniques on chewing in humans. _Nature_ 531, 500–503

(2016). Article  CAS  ADS  Google Scholar  * Carpenter, K. Biggest of the big: a critical re-evaluation of the mega-sauropod Amphicoelias fragillimus Cope, 1878. _New Mexico Museum of

Natural History and Science Bulletin_ 36, 131–137 (2006). Google Scholar  * Wings, O. & Sander, P. M. No gastric mill in sauropod dinosaurs: new evidence from analysis of gastrolith mass

and function in ostriches. _P. Roy. Soc. Lon. B. Bio._ 274, 635–640 (2007). Article  Google Scholar  * Sander, P. M. & Clauss, M. Sauropod Gigantism. _Science_ 322, 200–201 (2008).

Article  CAS  Google Scholar  * Hartstone-Rose, A., Perry, J. M. G. & Morrow, C. J. Bite force estimation and the fiber architecture of felid masticatory muscles. _Anat. Rec._ 295,

1336–1351 (2012). Article  Google Scholar  * Perry, J. M. G., Hartstone-Rose, A. & Wall, C. E. The jaw adductors of strepsirrhines in relation to body size, diet, and ingested food size.

_Anat. Rec._ 294, 712–728 (2011). Article  Google Scholar  * Taylor, A. B. et al. Jaw-muscle force and excursion scale with negative allometry in platyrrhine primates. _Am. J. Phys.

Anthropol._, 158, 242–256 (2015). Article  Google Scholar  * Anapol, F., Shahnoor, N. & Ross, C. F. _Scaling of reduced physiologic cross-sectional area in primate muscles of

mastication_. (ed. C. Vinyard ), Ch. 10, 201–216 (2008). Download references ACKNOWLEDGEMENTS The authors thank Chad Joines, Lisa Nulton, and Philip Keffer at Virginia Tech farms for

allowing the authors to videotape animals and measuring animal weights. Also, the authors thank Shmuel Rubinstein, Tobias Schneider, and L. Mahadevan for their encouragements, Sean Gart for

his help videotaping animals in the field, and Karina Jouravleva for help with data analysis. S.J. acknowledges support from the National Science Foundation (PHY-1205642) and the Virginia

Tech open access subvention fund. AUTHOR INFORMATION Author notes * Emmanuel Virot, Christophe Clanet and Sunghwan Jung: These authors contributed equally to this work. AUTHORS AND

AFFILIATIONS * Emergent Complexity in Physical Systems Laboratory (ECPS), École Polytechnique Fédérale de Lausanne, Lausanne, CH 1015, Switzerland Emmanuel Virot * John A, Paulson School of

Engineering and Applied Sciences, Harvard University, Cambridge, 02138, MA, USA Emmanuel Virot * Department of Biomedical Engineering and Mechanics, Virginia Tech, Blacksburg, 24061, VA, USA

Grace Ma & Sunghwan Jung * LadHyX, CNRS UMR 7646, École Polytechnique, Palaiseau, 91128, France Christophe Clanet * PMMH, CNRS UMR 7636, ESPCI, 10 rue Vauquelin, Paris, 75005, France

Christophe Clanet * Center for Soft Matter and Biological Physics, Virginia Tech, Blacksburg, 24061, VA, USA Sunghwan Jung Authors * Emmanuel Virot View author publications You can also

search for this author inPubMed Google Scholar * Grace Ma View author publications You can also search for this author inPubMed Google Scholar * Christophe Clanet View author publications

You can also search for this author inPubMed Google Scholar * Sunghwan Jung View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS E.V., C.C. and

S.J. conceived the research. E.V., G.M. and S.J. conducted the experiments and analyzed data. E.V., G.M., C.C. and S.J. wrote the manuscript. CORRESPONDING AUTHOR Correspondence to Sunghwan

Jung. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing financial interests. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION (PDF 55 KB) SUPPLEMENTARY VIDEO2 (AVI

9940 KB) SUPPLEMENTARY VIDEO3 (AVI 7283 KB) SUPPLEMENTARY VIDEO4 (AVI 13497 KB) RIGHTS AND PERMISSIONS This work is licensed under a Creative Commons Attribution 4.0 International License.

The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not

included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit

http://creativecommons.org/licenses/by/4.0/ Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Virot, E., Ma, G., Clanet, C. _et al._ Physics of chewing in terrestrial mammals.

_Sci Rep_ 7, 43967 (2017). https://doi.org/10.1038/srep43967 Download citation * Received: 11 November 2016 * Accepted: 01 February 2017 * Published: 07 March 2017 * DOI:

https://doi.org/10.1038/srep43967 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently

available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative